Strain or Tensile Test For Gauging Mechanical Properties

Maybe the most natural test of a material’s mechanical properties is the strain test, in which a strip or cylinder of the material, having length L and cross-sectional area A, is anchored at one end and the subject of an axial load P a load acting along the specimen’s long axis at the other.As the load is increased continuously, the axial deflection 948 ; of the loaded end will increase also. Finally the test example breaks or does something else devastating, regularly fracturing startlingly into a few pieces. ( Materials can fail mechanically in many alternative ways ; as an example, recall how blackboard chalk, a bit of fresh wood, and Stupid Putty break. )

As engineers, we naturally need to understand such matters as how fracture is related to P, and what final fracture load we would expect in an example of different size than the first one. As materials technologists, we feel like know how these relations are influenced by the constitution and microstructure of the material. One of the vital historic developments in our experience of material mechanical properties was the awareness that the power of a uniaxially loaded example is related to the size of its cross-sectional area.

This concept is reasonable when one considers the will to arise from the quantity of chemical bonds connecting one cross section with the one opposite to it as showed in Figure, where each bond is visualised as a spring with a certain rigidity and strength.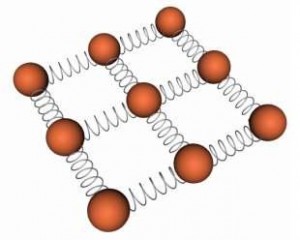

Manifestly , the amount of such bonds will increase proportionally with the section’s area1. The axial strength of a bit of blackboard chalk will thus increase as the square of its diameter. Against this, augmenting the length of the chalk won’t make it stronger ( in reality it’ll likely become weaker, since the longer sample will be statistically more certain to contain a strength-reducing failing. ) When reporting the power of materials loaded in strain, it is conventional to explain the effect of area by dividing the breaking load by the cross-sectional area where 963;f is the final tensile stress, frequently shortened as UTS, Pf is the load at fracture, and A0 is the first cross-sectional area.  Some materials exhibit substantial decreases in cross-sectional area as they seem to be stretched, and utilizing the original instead of last area gives the so-call engineering strength.

The units of stress are definitely load per unit area, N / m2 ( also called Pascals, or Pa ) in the SI system and lb / in2 ( or psi ) in units still used typically in the US.